Berechnungen und Zahlenmaterial

Techniken zur präzisen Vermessung und Berechnung der Cheops-Pyramide

Auf dieser Seite geht es darum, wie die Ägypter mit einfachen Mitteln eine unglaubliche Präzision bei der Vermessung erreichen konnten:
Ägyptische Masseinheiten - Grösse der Cheops-Pyramide in Königsellen gerechnet - Rechte Winkel - Kontolle des Neigungswinkels mit dem Seked - Nivellierung - Das Giza Plateau - Ausrichtung nach den Himmelrichtungen

Quellen - Zusatzinformationen - Interessante Links

Ägyptische Masseinheiten

Die Ägypter verwendeten Königsellen, Handbreit (Handflächen) und Finger als Masseinheiten. Dabei war eine Königselle in 7 Handbreit eingeteilt und ein Handbreit in 4 Finger also ergaben 28 Finger eine Königselle.

	1 Königselle = 52.4cm (Meh Nesut) = 7 Handbreit = 28 Finger [1]
	1 Handbreit = 7.48cm (Shesep oder Shep)
	1 Finger = 1.87cm (Yeba oder Zebo) Das Finger-Zeichen wird auch als 10'000 verwendet
	Da das Symbol für 100 (Khet oder Chet) ein gerolltes Seil ist nimmt man an, dass sie Vermessungschnüre brauchten, die 100 Königsellen massen (= 52.24m) [2].
	Hieroglyphe, die Messseil bedeutet. Zum Vermessen verwendeten die alten Ägypter Schnüre und Holzstäbe (Abbildung 1 / 2 Rekonstruktion).

Liste von Hieroglyphen

Grösse der Cheops-Pyramide in Königsellen gerechnet (wie die Ägypter)

Die alten Ägypter rechneten mit Königsellen, wobei eine Königselle 0.524m ist. Dadurch ergeben für uns unlogische Masse wie die Höhe von 146.59m plötzlich Sinn, denn dies sind exakt 280 Königsellen [5].
Die Grösse der Cheops-Pyramide, Bauleistung, Materialien

	Seitenlängen (a)		440 Königsellen
	Höhe (h)		280 Königsellen
	Höhe der Seitenflächen (c)		356 Königsellen (356.09)
	Diagonale (d)		622.25 Königsellen
	Gratlänge (g)		418.56 Königsellen
	Pyramidenwinkel α		51.843°
	Pyramidenwinkel β		58.3°
	Pyramidenwinkel γ		41.9°
	Eckwinkel		90°

Als Vergleich:
Die Chefren-Pyramide hat eine Basis von 410 mal 410 Ellen und ist 275 Ellen hoch (= Neigungswinkel von 53.29°), die Mykerinos-Pyramide hat eine Basis von 200 mal 200 Ellen und ist 125 Ellen hoch (= Neigungswinkel von 51.34°). Übrigens sind die Diagonale (Mykerinos = 282 Ellen) bezw. die halbe Diagonale (Chefren = 289 Ellen) je etwas mehr als die Höhe der Cheops-Pyramide (280 Ellen)

Rechte Winkel in den Ecken

Die Grundfläche der Cheops-Pyramide bildet ein vollkommenes Quadrat - die Abweichung vom 90°-Winkel ist maximal eine Minute - wie wurden die rechten Winkel so perfekt bestimmt?

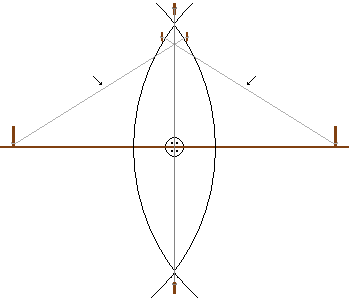Die erste Möglichkeit, um einen rechten Winkel zu bestimmen ist mit einem Zirkelschlag die Mittelsenkrechte zu bestimmen. Die Ägypter benutzten zwei Pfosten an denen je ein Seil der gleichen Länge befestigt wurde (die Seile mussten etwas länger als die Hälfte der Strecke messen). Nun konnte ein Halbkreis gezogen werden. An den zwei Punkten, wo sich die Seile schnitten wurde eine Senkrechte gezogen. Diese bildete zur Verbindungslinie einen rechten Winkel und teilte die Strecke in zwei gleiche Teile.

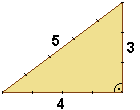
Man kann davon ausgehen, dass die Ägypter zwar nicht die Theorie hinter dem Satz des Pythagoras (a² + b² = c²) kannten, aber die praktische Anwendung für die Vermessung von Bauwerken und Land durchaus beherrschten. Die Ägypter kannten die so genannten pythagoreische Tripel, das sind Gruppen von drei natürlichen Zahlen, die als Längen der Seiten eines rechtwinkligen Dreiecks vorkommen können. Die Zahlen 5-4-3 sind ein pythagoreisches Tripel, wobei 5²=4²+3² (25=16+9).

So weiss man, dass Landvermesser, die so genannten Harpedonapten (übersetzt "ich binde" oder "ich spanne") mit Hilfe von Zwölfknotenschnüren genaue rechte Winkel vermessen konnten. Das dabei verwendete Seil wurde durch Knoten (oder mit Farbmarkierungen) in 12 gleiche Teile unterteilt. Mit dieser Schnur bildeten sie ein rechtwinkliges Dreieck mit den Seiten 3:4:5. Das ist wohl, welches das bekannteste pythagoräischen Tripel (von 3² + 4² = 5²). Diese Methode wandten die Seilspanner vor allem an, wenn die Schlammfelder nach dem Rückgang der Nilfluten neu abzumessen waren.

Für die Bestimmung der rechten Winkel der Pyramidengrundfläche konnte dieses System ebenfalls verwendet werden [13]. Zur Kontrolle der gesamten Pyramidengrundfläche mussten jedoch sehr grosse Distanzen (230m) abgemessen werden, ausserdem verhinderte der Felskern in der Mitte die Ausmessung der Diagonale. Bei diesen grossen Distanzen muss angenommen werden, dass Seile dieser Länge zu sperrig (für ein 3-4-5 Dreieck mit den Massen von 75-100-125 Ellen ergäbe das eine Länge von 156m) und auch zu wenig genau wären. Für das Messen der Distanzen wurden deshalb wahrscheinlich Stäbe einer gewissen Länge verwendet, so dass genauere Ergebnisse erziehlt werden konnten. Vorgeschlagen werden Stäbe von 4 oder 8 Ellen (2 bis 4m).
Abbildung 1 / 2 (Detail) eines Seilspanners aus dem Grab von Menna (hier sind die Knoten sichtbar, die eine Elle auseinanderliegen [2])

Interessante mathematische Beziehungen ergeben sich auch, wenn man die Masse der Königskammer der Cheops-Pyramide hinsichtlich des Lehrsatzes von Pythagoras anschaut.
Königskammer, Grosse Galerie und Entlastungskammern (Details)

Kontrolle des Neigungswinkels mit dem Seked

Es ist sehr wichtig, dass der Neigungswinkel einer Pyramide über den ganzen Pyramidengrat gleich bleibt und dass alle Seitenflächen den gleichen Neigungswinkel haben. Fehler bei der Einhaltung des Neigungswinkels hatte starke Auswirkungen auf die Form der Pyramide.
Vermessungsprobleme und die Auswirkungen auf die Form der Pyramide

Es ist äusserst wichtig, dass die äusseren Steine bereits während des Zurichtens im Steinbruch von Tura auf die richtige Schräge bearbeitet und geglättet werden und nicht erst auf der Pyramide. Nach Franz Löhner wird dieser Winkel schon im Steinbruch aufs Genauste eingemessen und dann wird nochmals jeder äussere Tura-Stein in der Bauhütte auf Pyramidenebene kontrolliert und mit Hilfe von speziellen Lehren nachgemessen. Nachdem die Steine auf die gewünschte Höhe gezogen worden sind, werden die äusseren Steine aufeinandergelegt und hier nochmals der genaue Winkel kontrolliert. Ausserdem kann man durch Auflegen einer geraden Planke kontrollieren, ob die Seitenfläche auch flach und ohne Wölbung ist. Ebenso wird bei den wichtigen Ecksteinen durch das Spannen einer Schnur (oder dem Auflegen einer Holzlatte) kontrolliert, ob der Pyramidengrat gerade verläuft. Nach Vollendung jeder Steinschicht kann die Oberfläche des Pyramidenkegels genaustens ausgemessen werden und so kann kontrolliert werden, ob die Ecken wirklich rechtwinklig und die Seitenlängen gleich gross sind. Werden Fehler festgestellt so können sie jetzt noch behoben werden, etwa indem ein Stein falls nötig ausgetauscht oder falls noch möglich präziser zugehauen wird.
Steinbrüche im alten Ägypten (Details zu Lehre)
Äussere Steine - Glättung von unten nach oben?

Die Ägypter kannten keine Einteilung der Winkel in 360°. Aus dem mathematischen Rhind Papyrus wissen wir, dass die Ägypter mit so genannten seked (seqt, seqed oder sqd) rechneten. Dabei wird nicht der Winkel der Neigung gemessen, sondern der Rücksprung (horizontale Versetzung) der Mauer. Das heisst es wird gemessen, um wieviele Handbreit und Finger die obere Kante der Mauer zur unteren Kante zurückversetzt ist, und zwar bei einer Höhe von einer Elle.

Für die Seitenfläche der Cheops-Pyramide ist der seked 5½ Handbreit. Das heisst auf einer Königselle Höhe ist die obere Kante um 5½ Handbreit (= 22 Finger) zurückversetzt, was einen Neigungswinkel von 51.84° ergibt. In Grad ausgedrückt sind das 51°50'24''. Dies entspricht mit einem winzigen Unterschied der offiziellen Messung des Cheops-Neigungswinkels von 51°50'40'' [5].
Berechnet man mit diesen Seitenverhältnissen ein rechtwinkliges Dreieck mit möglichst kleinen ganzen Zahlen, so wählen wir a=11 und b=14 was c=17.8 ergibt (dies ist kein pythagoreisches Tripel). Schaut man die Höhe (280 Ellen) und Seitenlängen (Hälfte = 220 Ellen) der Cheops-Pyramide an, so findet man hier das Verhältnis 14 :11 selbstverständlich auch wieder. Pythagoreische Tripel Die Ägypter verwendeten den seked für viele ihrer Bauwerke. Die Chefren-Pyramide hat einen seked von 5 Handbreit und 1 Finger (oder 3-4-5 / 53.1° = 51°06'). Die Djedefre Pyramide hat einen seked von 4 Handbreit (4-7-8 / 60.2° = 60°12') [10].

Nivellierung der Pyramiden-Grundfläche

Bei der Cheops-Pyramide wurde um den bestehenden Felskern der Grund eingeebnet und durch ein präzise verlegtes Fundament eine Ebene hergestellt, die einen maximalen Höhenuntersschied von nur 2.1 cm aufweist [11]. In der Mitte der Grundfläche wurde der Felsen noch stehengelassen. Dies ist eine bemerkenswerte Leistung, wenn man bedenkt, dass es wegen des Felskerns nicht möglich war, die Diagonale des Pyramidenquadrats zu messen.
Vermessungsprobleme und die Auswirkungen auf die Form der Pyramide
Die Bauphasen auf der Pyramiden-Baustelle (Felskern)

Die alten Ägypter kannten die Setzwaage, das ist ein gleichschenkliges rechtwinkliges Holzdreieck, dass sie als Nivellierinstrument verwendten. Dieser A-förmige Holzrahmen sieht ähnlich wie ein Geometriedreieck oder eine Winkellehre aus. Ein Senklot hängt genau in der Mitte hinunter. Wenn sich das von der Winkelspitze des "A" hängende Senkblei mit der Markierung in der Mitte des Querbalkens deckt, ist die Oberfläche, auf der die Schenkel stehen, eben. Wird das Dreieck direkt auf einen Stein daraufgesetzt, so kann auf einfache Weise der Stein nivelliert werden.

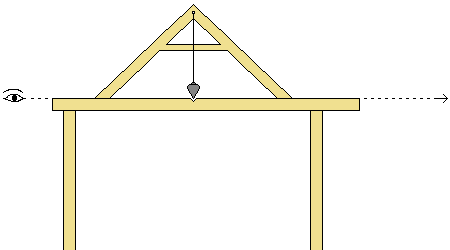
Gleichschenkliges Holzdreieck mit Senklot und Senkblei, dass auf die Markierung auf dem Querbalken zeigt.

Zur Nivellierung von grösseren Distanzen kann dieses Holzdreieck auf Balken gelegt werden. Nach dem Ausrichten des Dreiecks kann durch Anvisieren über den Querbalken bestimmt werden, ob in der Distanz eine Messlatte die gewünschte Höhe anzeigt. Versuche ergaben, dass auf einer Distanz von 45m bis auf einen Zentimeter genau gemessen werden konnte [8]. Grössere Distanzen gehen nicht, da dann das menschliche Auge zu wenig genau sieht. Da man von einer solchen Messeinrichtungen aus auf beide Seiten messen kann, sollte es möglich gewesen sein, Distanzen von bis zu 90 Metern exakt zu nivellieren. Man kennt drei Funde solcher Holzdreiecke, etwa aus dem Grab von Sennedjem in Deir el-Medineh.

Ein weiterer Vorschlag von einigen Ägyptologen beinhaltet, dass niedrige Gruben um das zu nivellierende Gelände gegraben und mit Wasser gefüllt werden. Indem der Wasserspiegel an mehreren Stellen markiert wird, und diese Punkte verbunden werden, ist eine Referenzlinie für die Nivellierung geschaffen. Dieser Vorschlag ist jedoch nicht sehr leicht umsetzbar, erstens da der Nil und der Nilkanal rund 44m tiefer unten verlaufen und zweitens, da das Wasser entweder in den Gruben versickern oder verdunsten würde, schliesslich wurden die Pyramiden in der Wüste gebaut.

Das Giza Plateau in Übersicht (Karte)

Die Pyramiden sind exakt nach den vier Himmelsrichtungen ausgerichtet. Zwischen den Haupt-Pyramiden (inkl. Königinnen-Pyramiden) lassen sich Fluchtlinien ziehen, die die östlichen Ecken der Pyramiden untereinander verbinden [3].
Karte mit GPS-Koordinaten / Google Earth Foto der Pyramiden

Karte der Giza (Giseh) Ebene mit Höhenlinien nach GPMP [12]. 100m = 191 Königsellen. Blau = Fluchtlinien

Diese exakte Ausmessung konnte nur durch genaue Messtechniken und einer präzisen Berechnung erreicht werden. Fehler bei der Vermessung hatten oft grosse Auswirkungen auf die Form der Pyramide.
Vermessungsprobleme und die Auswirkungen auf die Form der Pyramide

Ausrichtung nach Norden

Die Ausrichtung der Cheops-Pyramide nach Norden ist erstaunlich präzise (Abweichung nur 2' 28''). Um diese Genauigkeit der Ausrichtung zu erreichen gibt es verschiedene Vorschläge. Der wohl einleuchtenste Vorschlag ist derjenige von Otto Neugebauer [6]. Diese simple Technik geht folgendermassen:

Ein präzise gearbeitetes kleines Pyramidion (z.B. aus Holz oder Stein) wird auf ungefährer Nord-Süd-Lage auf den ebenen Bauuntergrund gelegt. Zwei der Kanten werden auf der Schattenseite als Linien verlängert eingezeichnet. Während eines Tages wird genau beobachtet, an welchen Punkten der Schatten des Pyramidions diese beiden Linien schneidet. Das Pyramidion ist präzise in Nord-Süd Richtung ausgerichtet, wenn beide Abschnitte (Strecke Schnittpunkt - Pyramidenecke) absolut gleich gross sind. Um das zu erreichen experimentiert man über mehrere Tage mit dem Pyramididon, bis dies eintrifft. Zur Kontrolle verschiebt man das Pyramidion auf dem Pyramidenplateau und wiederholt die Messungen an verschiedenen Messpunkten. Sogar noch während des Baus können die Messungen oben auf dem wachsenden Pyramidenstumpf wiederholt werden, falls eine flache Oberfläche zur Verfügung steht.

Diese Messungen müssen durchgeführt werden, wenn die Sonne nicht höher als 52° im Himmel steht, da ein 52°-Pyramididon nur dann einen Schatten wirft (alleinfalls muss man ein steileres Pyramidion wählen). Dies ist in den Wintermonaten leichter, da dann die Sonne tiefer steht. Genaue Zahlen.

Ausserdem wird vorgeschlagen, dass zur weiteren Justierung nun eine der kleinen Nebenpyramide errichtet wird (südlich der Cheops-Pyramide liegt die kleine Pyramide G1d, die 23 x 23m =44 Ellen, was einem Zehntel der Seitenlänge der Cheops-Pyramide von 440 Ellen entspricht) gross ist und einen 52° Neigungswinkel hat [5]. Indem weitere Messungen in der gleichen Weise durchgeführt werden kann die Nord-Süd-Ausrichtung mit noch höherer Präzision bestimmt werden. Eine weitere Kontrolle durch die Königinnen-Pyramiden, die ebenfalls einen Neigungswinkel von 51°-52° haben [5] wäre ebenfalls möglich gewesen. Auch Ägyptologen geht davon aus, dass die abgesteckte Nordsüdrichtung gleich der Ostkante der Pyramide war und nicht die Mittellinie durch die Spitze, da letztere wegen des Felsenkerns nicht auszumessen gewesen wäre [4].
Mehr Informationen über die Neben- oder Satellitenpyramiden
Die Bauphasen auf der Pyramiden-Baustelle

Ein weiterer, etwas komplizierterer Vorschlag stammt von I.E.S. Edwards [7]. Gemäss seiner Theorie bauten die Ägypter eine kreisfömige und oben absolut waagrechte Mauer, die einen künstlichen Horizont bildete. Mit Hilfe eines Visierinstrumentes konnte nun der Auf- und Untergang eines horizontnahen Sterns gemessen werden und auf dem künstlichen Horizont markiert werden. Daraus ergaben sich dann drei Messpunkte, der Mittelpunkt, der Sternaufgangspunkt (A), und Sternuntergangspunkt (B). Diese wurden dann per Senklot zum Mauerfuss verlängert und mit der Kreismitte verbunden. Norden lag genau in der Mitte des Winkels, den diese beiden Linien einschlossen. Abbildung

Quellen

[1] M. Clagett Ancient Egyptian Science - Volume 3 Ancient Egyptians Mathemathics
[2] D. Arnold Building in Egypt
[3] M. Lehner The Complete Pyramids of Egypt
[4] R. Stadelmann Die grossen Pyramiden von Giza
[5] D. Arnold Lexikon der Ägyptischen Baukunst
[6] O. Neugebauer On the orientation of pyramids
[7] I.E.S. Edwards The Pyramids of Egypt
[8] D. Arnold Building in Egypt: D. Arnold und M. Isler verwendeten dabei ein 2m langes Querholz und das beschriebene Nivellierungsdreieck
[9] J. Ph. Lauer Oberservations sur les pyramides
[10] C. Rossi Architecture and Mathematics in Ancient Egypt
[11] L. Borchardt Längen und Richtungen der vier Grundkanten der großen Pyramide bei Gise
[12] Giza Plateau Mapping Project GPMP
[13] J. Ph. Lauer Le Triangle Sacré das les plans des monuments de l'Ancient Empire

Zusatzinformationen

Kairo (Ägypten): Sonnenstand (oben Kairo, Ägypten eingeben) / Überblick alle Monate

Begriffe:
Die Sonnenhöhe wird in Grad angegeben. Null Grad bedeuten, dass die Sonne gerade den Horizont berührt und 90 Grad, dass die Sonne senkrecht über dem Betrachter steht.

Interessante Links

Im unter [1] aufgelistetem Buch sind verschiedene mathematische Papyri abgebildet und auf englisch erklärt (Rhind, Moskauer, Kahun, Reisner, Berlin, British Museum). Ausserdem hat es Abbildungen von mehreren Ellen-Stäben (Cubit-rods).
Englischer Text "Tools and Their Application" zum Thema Vermessung von D. Arnold
Der Rhind Papyrus zum Thema "Genaues Rechnen. Einführung in die Kenntnis aller existierenden Gegenstände und aller dunklen Geheimnisse" des Schreibers A’h-mosè (Ahmes)
Englische Übersetzung und Erklärungen zur Mathematik auf dem Rhind-Pypyrus

Impressum:	Copyright 2006:	Franz Löhner www.cheops-pyramide.ch
	Seitentext und Illustrationen:	Teresa (Zubi) Zuberbühler www.starfish.ch

This page in English