The Great Pyramid of Khufu (Cheops)
Alignment of the pyramids and controlling the shape of the pyramid
On this page various methods of the ancient Egyptians for surveying and
measuring are explained.
Survey and controlling - Obtaining
a pyramid shape - Possible mistakes while building
a pyramid - Egyptian units of measurement - Determining
right angles - Angle of inclination and seked
- Precise North-South alignment - Sources
Survey and controlling
The pyramid builders carefully chose the building ground for the pyramids. The Khufu-pyramid lies on the best ground existing on the Giza plateau and on top of a rock core which reaches to at least 7.9m height under the pyramid. How important the choice of building ground was, shows the fact, that one of the satellite pyramids (G1c) probably had to be moved closer to the others, because the ground was considered not stable enough.
 Major
problems had developed earlier at other building sites, because the strength
of the ground was overestimated when erecting a pyramid. For example the
ground beneath the pyramid of Sneferu (father of Khufu) in Dahshur gave
way under the weight and caused damage in the casing. Another outer layer
of casing had to be added, changing the angle of inclination from 60°
to 54.46°. But again structural problems with the subsidence developed,
the casing slipped and more damage occurred. In the end the angle of inclination
had to be drastically lowered to 43.99° [6].
Now this pyramid is called the Bent Pyramid, because of its shape.
Major
problems had developed earlier at other building sites, because the strength
of the ground was overestimated when erecting a pyramid. For example the
ground beneath the pyramid of Sneferu (father of Khufu) in Dahshur gave
way under the weight and caused damage in the casing. Another outer layer
of casing had to be added, changing the angle of inclination from 60°
to 54.46°. But again structural problems with the subsidence developed,
the casing slipped and more damage occurred. In the end the angle of inclination
had to be drastically lowered to 43.99° [6].
Now this pyramid is called the Bent Pyramid, because of its shape.
![]() The outer casing stones of the pyramid
The outer casing stones of the pyramid
A survey of the Giza plateau shows that the pyramids are aligned to the north-south axis as well as in relation to each other. The ancient engineers worked very precisely, not only are the three pyramids each perfectly centered, but the angle of inclination is also the same from bottom to top [4].
Map: The Giza Plateau with the Great Pyramids GPMP [8]. 100m=191 cubits. Map with GPS-Coordinates
 Obtaining a pyramid shape
Obtaining a pyramid shape
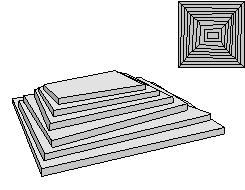
A pyramid is a simple shape but when building a pyramid structure as large as the pyramid of Khufu there were a lot of obstacles to overcome.
It was imperative to build the pyramids with a technique where
these factors could be controlled at all times. With ramps covering
the pyramid flanks this would have lead to major problems. This
is no problem at all, if you use Löhner rope roll stations
and tracks on the pyramid flank.
|
||
|
|
|
| Center The center of the pyramid is moved to the side. The pyramid looks lopsided. |
Right angles If the angles are not the same (for example 90°), the center of the pyramid moves and the overall shape is distorted. |
|
|
|
|
| Edges / Corners The edges are not positioned in such a way as to form in a constant angle. The shape of the pyramid is totally distorted. The stones lying in the very middle and the corner stones were layed down specially carefully and then those stones would provide a guide to ensure the geometrical accuracy of the four right angled corners and the outer stones between. [3]. |
Angle of inclination If the angle of inclination is not controlled the lateral surfaces of the pyramid are either convex or concave. This was guaranteed, if the outer stones were cut already to the right angle in the quarry and were strictly controlled before they were brought to the pyramid. |
|
|
|
|
| Height and base The pyramid is determined by its height and the base. |
Smoothness The casing blocks have to present a smooth lateral surface. To achieve this the outer stones were specially well polished and all the joints filled. |
|
|
|
|
| Stability For more stability some stone layers are slightly tilted towards the center |
Alignment For religious reasons the pyramids on the Giza plateau are all aligned exactly north-south and in relation to each other |
|
 Egyptian units of measurement
Egyptian units of measurement
The ancient Egyptians used cubits, palms and fingers as units for measuring. The cubit was divided into 7 palms and a palm into 4 fingers which resulted in 28 fingers for one cubit.
| 1 cubit = 52.4cm (Meh Nesut) = 7 palm = 28 fingers [1]. Dimensions of the pyramid of Khufu in Royal Cubits |
||
| 1 palm = 7.48cm (Shesep or Shep) | ||
| 1 finger = 1.87cm (Yeba or Zebo) The hieroglyph of a finger is also used for the number 10'000 |
||
| Because the hieroglyph for 100 (Khet or Chet) is a rolled up rope some archaeologists think, that measuring ropes of 100 cubits were used (= 52.24m) [2]. | ||
Hieroglyph which signifies measuring rope.The Egyptians used ropes and rods for measuring (photo 1 / 2 reconstruction). |
 Determining right angles
Determining right angles
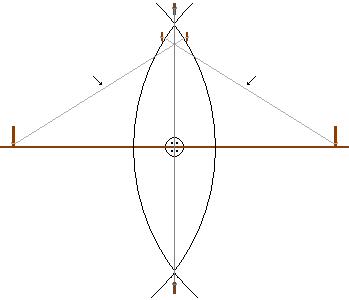 By stretching a cord between two pegs stuck in the ground, a long straight
line was marked out. Then to each peg an equal length of string was tied,
more than half as long as the line drawn. By keeping the strings stretched
tight and moving the ends around, the Egyptians could draw parts of two
perfect circles. These arcs cross each other at two points. By drawing
a straight line between these two points the original line is bisected
at a right angle and the line is cut into two equal parts.
By stretching a cord between two pegs stuck in the ground, a long straight
line was marked out. Then to each peg an equal length of string was tied,
more than half as long as the line drawn. By keeping the strings stretched
tight and moving the ends around, the Egyptians could draw parts of two
perfect circles. These arcs cross each other at two points. By drawing
a straight line between these two points the original line is bisected
at a right angle and the line is cut into two equal parts.
The Egyptians didn't know the theory explaining the Pythagorean theorem but they knew from experience, that they could form right angles by using a so called primitive Pythagorean triple. One of the most well well-known example of a Pythagorean triple is 3-4-5 where 3²+4²=5² (9+16=25).
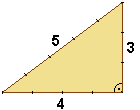 We
know, that the Pharaoh employed land surveyor, so called harpedonaptai
or harpedonapts (rope stretchers or rope-knotters). After the annual flooding
of the Nile river, when rich silt was deposited on the valley floor, the
property boundaries of the fields were destroyed, so they had to be reestablished.
The harpedonaptai used measuring cords with 11 equally spaced knots (or
marked with paint) dividing it into 12 parts. With these ropes they could
form a right triangle with the sides of 3:4:5.
We
know, that the Pharaoh employed land surveyor, so called harpedonaptai
or harpedonapts (rope stretchers or rope-knotters). After the annual flooding
of the Nile river, when rich silt was deposited on the valley floor, the
property boundaries of the fields were destroyed, so they had to be reestablished.
The harpedonaptai used measuring cords with 11 equally spaced knots (or
marked with paint) dividing it into 12 parts. With these ropes they could
form a right triangle with the sides of 3:4:5.
The same principle could be used to determine the right angle at the
base area of the pyramid of Khufu. These are very exact - the maximum
deviation from 90° is only one minute! [5]
Since the ropes might have been too bulky to measure such long distances
it is also possible, that wooden cubit rods were used instead.
![]() Illustration
of a rope stretcher from the tomb of Menna (here knots in the rope are
visible, they probably divide it in distances of 1 cubit [2])
Illustration
of a rope stretcher from the tomb of Menna (here knots in the rope are
visible, they probably divide it in distances of 1 cubit [2])
![]() Chapter
"Tools and Their Application" from a book by D. Arnold
Chapter
"Tools and Their Application" from a book by D. Arnold
 The angle of inclination and the seked
The angle of inclination and the seked
As shown above it was very important to control
the angle of inclination of the pyramid sides and the pyramid ridge.
Any mistakes had a major effect on the shape of the pyramid.
So it was important, that the outer stones were already
bevelled to the right angle in the Tura quarries and not
on the pyramid plateau, where there was not enough time and room
to accomplish this important task. According to Franz Löhner
this angle is already measured as exact as possible in the quarry
and then again controlled at the building yard at the foot of the
pyramid with the help of a special
wooden gauge. When the stones have arrived at the required height,
the outer stones are placed on top of each other and the angle and
the exact fit is checked again. By placing a wooden plank on top
of the surface you can also control, if the surface is level or
concave. The fit of the important corner stones can be controlled
by stretching a rope along the pyramid ridge (or by placing a plank
on top). After finishing each stone course the surface of the pyramid
frustum is measured, the corners checked if they measure exactly
90 degrees and if the length of the four edges are the same. If
mistakes are found, they can still be corrected, either by replacing
a stone or by cutting it to a better shape.
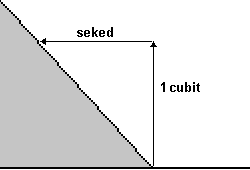
For the angle of inclination of the sides of Khufu's pyramid the
seked is 5½ palms. With other words, if the wall is 1 cubit
high the upper edge is offset by 5½ palms (= 22 fingers)
which gives an angle of inclination of 51.84° or 51°50'24''.
This is - with a tiny difference - just the official angle of inclination
of the pyramid of Khufu which is given as 51°50'40'' [5].
|
|
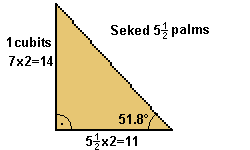 |
 |
If we want to calculate a right triangle with this
width-to-height ratio using numbers as small as possible we choose
a=11 and b=14 which transfers into c=17.8 (this isn't a Pythagorean
triple). If we look at the height (280 cubits) and the side length
(half = 220 cubits) of the pyramid of Khufu, of course we find the
width-to-height ratio of 14 :11 again. The Egyptians used the seked for many other buildings. The Khafre
pyramid has a seked of 5 palms and 1 finger (or 3-4-5 / 53.13°
= 51°06'). The Djedefre pyramid has a seked of 4 palms (4-7-8
/ 60.2° = 60°12') [7]. |
|
 Leveling a base area for the pyramid using a square level
Leveling a base area for the pyramid using a square level
The base area or plateau of the pyramid of Khufu (including the surrounding
pavement) was leveled with great precision, so only a deviation of 2.1
cm can be measured [4]. In the middle of the base
area a rock core was left.
![]() The pyramid building yard - the center of
the construction project
The pyramid building yard - the center of
the construction project
The only instrument for leveling known to the ancient Egyptians was the square level. This is a right-angled isosceles triangle made from wood. This tool is made in the shape of the letter "A" and looks like a triangle ruler or a builder's square. A plumb-line is suspended from the top of the connected corners. If the plumb bob coincides with a mark in the middle of the crossbeam, the surface area on which the two legs stand is level. By placing this triangle on stone, these could be easily leveled.
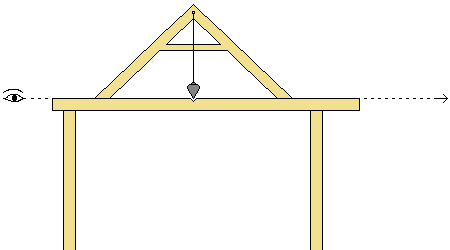
Isosceles triangle made from wood with plumb-line and plumb bob, which points to the mark on the cross beam.
For establishing equal levels over large distances, this triangle was laid on top of a beam. First the triangle was checked and adjusted, so it would lie horizontally and level on the beam. Then, by fixing upon a leveling staff in the distance, differences in height could be noticed and corrected. Field tests showed, that up to a distance of 45m a difference of 1 centimeter could be detected [8]. Because of the limited eye sight of humans larger distances could not be covered. But because it is possible to sight on both sides from this kind of measuring station, it probably was possible to correctly level distances of up to 90 meters. Level squares like we described here were found for example in the tomb of Senedjem at Deir el-Medina.
Another suggestion made by some archaeologists is to dig flat ditches surrounding the pyramids and then filling them with water. At the top of the water's surface, the level would be marked along the sides of the ditches as a reference. Other archaeologists object, that the Nile and the Nile channel run about 44m lower and that water evaporates quickly in the desert. They think, this kind of leveling method could not have been used.
 Precise North-South alignment
Precise North-South alignment
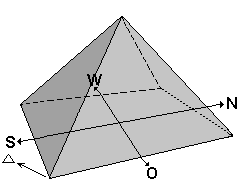
The Great Pyramid's north-south axis is nearly aligned to true north, the deviation is only 2' 28''. To achieve this precision the Egyptians had to make an exact survey and do control measurements. Otto Neugebauer [1] is offering a simple solution to this problem.
A small but precisely worked pyramidion (made from wood or stone) is placed as close as possible to a north-south position on the flattened ground where the pyramid will be built. Then two lines are drawn, taking the edges of the small pyramidion and lengthening them on the side which lies in the shadow. During a day a surveyor notes down, where exactly the tip of the pyramid shadow cuts through those two lines. The pyramidion is precisely aligned north to south, when both lines are cut at the same distance to the corner of the pyramidion. To achieve this, the pyramidion is moved slightly over a period of days, until both segments are exactly the same length. Since the pyramidion can be moved, the process can be repeated at several places on the pyramid plateau, thus checking and rechecking the north-south alignment. Even during the construction of the pyramid, when working on the pyramid frustum, this system can be used again for checking, if the surface is smooth enough, for example on top of the pyramid plateau.
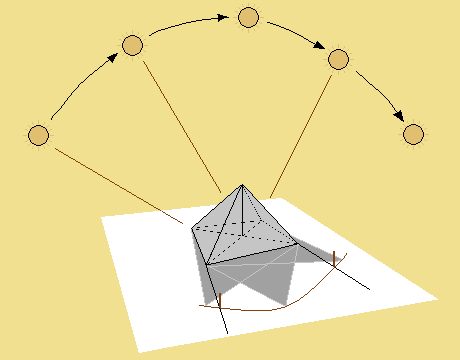
How to determinate the north-south alignment of a pyramid
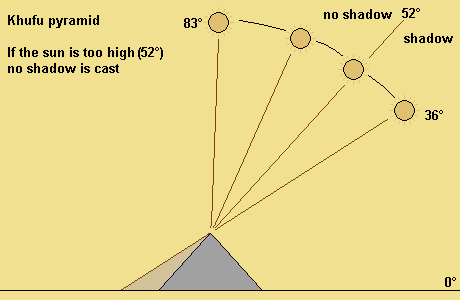
It is easier to make those measurements during the winter months, when the sun is lower in the horizon, because during the summer months the pyramids don't cast a shadow during large parts of the day.
For further precision you can now build a small but accurately shaped pyramid. South of the pyramid of Khufu lies a small pyramid (G1d) which measures 23 times 23m and has an angle of 51-52° [2]. This pyramid or one of the queen's pyramids could possibly have been used to further adjust the north-south-alignment using again the same process described above but with slight alterations.
Another, a bit more complicated suggestion was made by I.E.S. Edwards. According to his theory the Egyptians built a circular wall whose top was carefully leveled, thus creating an artificial horizon. From a straight pole with a forked top in the center sightings were made to determine, where exactly a certain circumpolar star was rising and setting. Using a plumb line the positions were marked on bottom of the wall. By bisecting those positions, true north was provided [3]. Illustration
 Sources
Sources
[1] O. Neugebauer
On the orientation of pyramids
[2] D. Arnold Lexikon
der Ägyptischen Baukunst
[3] I.E.S. Edwards The Pyramids
of Egypt
[4] M. Lehner The Complete Pyramids
of Egypt
[5] R. Stadelmann Die grossen
Pyramiden von Giza
[6] This is the real reason and not as some authors claim, that Senefru
run low on money before the pyramid was completed! He actually build a
second one close by - the Red Pyramid.
[7] C. Rossi Architecture and Mathematics
in Ancient Egypt
[8] Giza Plateau Mapping Project GPMP
Cairo (Egypt): Sun's
location / Overview
all months
Shortest day (22. December):
Peak altitude of the sun (top culmination) 36°
Lowest sun's altitude (lower culmination point) -83°
Longest day (21. June):
Peak altitude of the sun (top culmination) 83°
Lowest sun's altitude (lower culmination point) -36°
Explanation:
The altitude of the sun is given in degrees, with zero degrees meaning
a position of the sun on the horizon and 90 degrees meaning a vertical
position of the sun in relation to the observer.
| Copyright 2006: |
Franz Löhner www.cheops-pyramide.ch | |
| Concept and Design, English Texts: |
Teresa (Zubi) Zuberbühler www.starfish.ch |
Diese Seite auf Deutsch (Pyramidenform - Vermessungstechniken)
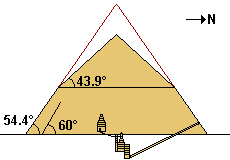
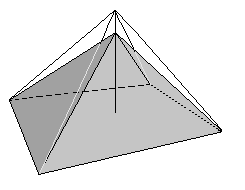
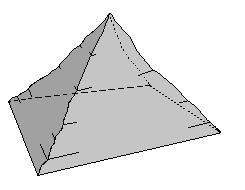
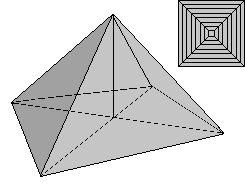 A
pyramid is determined by its base and height. The
base chosen for Khufu's pyramid is square and right-angled. The
height was determined in advance, so the sides of the pyramid nearly
form an equilateral triangle and the pyramid is exactly aligned
to the four cardinal point. But while building the pyramid of Khufu
several additional factors had to be measured and calculated throughout
the building process: the angle of the lateral surfaces, the ridge
and the position of the corners. Matters of stability also had to
be taken in consideration (see
A
pyramid is determined by its base and height. The
base chosen for Khufu's pyramid is square and right-angled. The
height was determined in advance, so the sides of the pyramid nearly
form an equilateral triangle and the pyramid is exactly aligned
to the four cardinal point. But while building the pyramid of Khufu
several additional factors had to be measured and calculated throughout
the building process: the angle of the lateral surfaces, the ridge
and the position of the corners. Matters of stability also had to
be taken in consideration (see 
 From
the
From
the